Determining what happens to a pair of curling rocks after one hits another is a relatively simple physics/geometry problem: they’re basically circles moving on a flat plane, they have basically the same mass, and one of them starts stationary. For some of you (those who liked geometry or play pool), you’ve got this well in hand. For some of you, you’re slumping in your chairs already afraid I’m going to use numbers and formulas, and well, a little of that is coming.

Let’s say you have a PhD in a field that ends in -physics, but go to Wikipedia to refresh your memory of the formulas for a basic collision. Hypothetically speaking (no, of course for real and not hypothetically, just like librarians still have to sing the alphabet song, physicists often have to refresh their memory of super basic concepts on Wikipedia. To be fair, it’s why so many of those articles are so detailed).

That hypothetical description would start with “For the case of two non-spinning colliding bodies…” and while one of our rocks is going to start with a rotation, we’ll deal with how it changes things later – let’s get a good enough, simple understanding of angles to start.

Wikipedia’s description of how the collision works is really good, but uses a lot of physics-y words. Basically, at the point the rocks make contact, you can draw a line between their centres, and one perpendicular (square) to that – this is called the tangent.

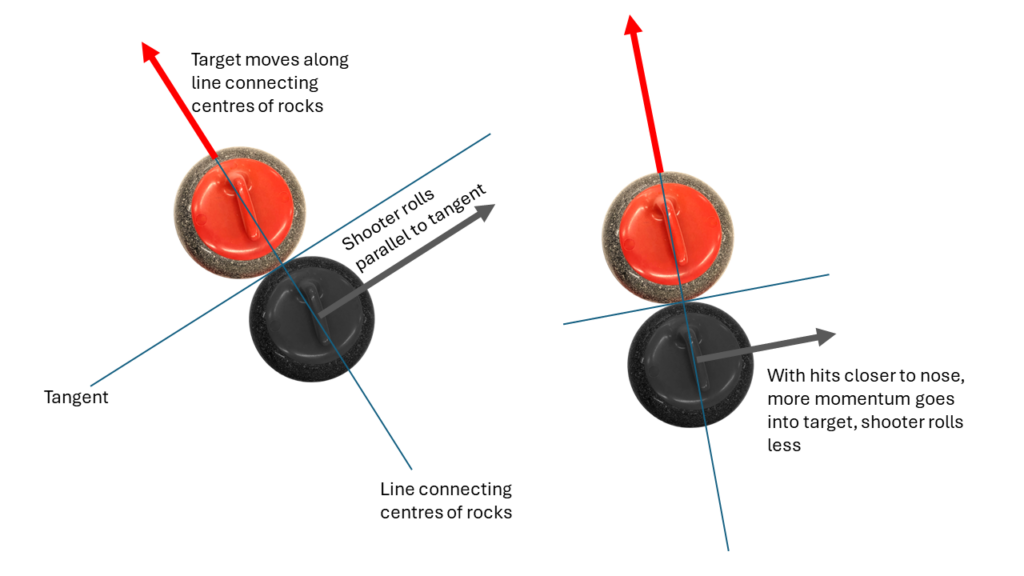
The rock being hit is going to move along the line that connects the two centres. This is the main take-home message so it’s in bold. The second thing to know is that the moving rock making the hit (usually the shooter but for double-take-outs it could be the first rock hit, or any prior rock if there’s a lot of granite moving) is going to be deflected and move along the tangent.

There’s some math involved to figure out how much of the original energy gets transferred to the stationary rock and how much the shooter keeps, but generally you can take an educated guess at that and be close enough.

A “nose hit,” where the shooter hits the target right in the middle on the line the shooter is moving on is going to have all the momentum transferred to the target stone, and the shooter will stop dead in its tracks: a hit-and-stick as we call it in curling. As hits get thinner, we will then see the target deflected more sideways (with a decreasing fraction of the energy) and the shooter being deflected less and less, keeping more of the original energy.

A “half rock” hit is going to have that tangent be just about 60 degrees: both rocks will move out with a fair bit of energy, though more of the original energy will go into the target rock. And so on until a rock just barely brushes the target on the way by.

[Side note: I made a rookie error by not actually doing the trigonometry and said a half rock would be 45 degrees in the first version of this post, which was not correct — it’s 60 degrees]

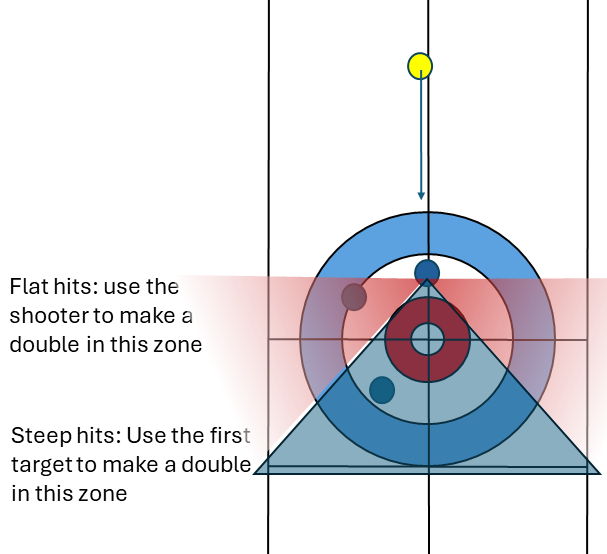
To line up a double-takeout, we just keep these basic ideas in mind, and work backwards from the final rock we want to hit: line up through the centre of the final rock to the first rock. Then figure out where to hit the first rock to either have the shooter bounce off to hit your final rock, or have the first rock come hit the second rock.

When deciding whether you want to have the shooter or the target be the rock that hits the second rock, consider how “steep” the setup is for the double-takeout. If the second target is nearly perfectly behind the first target (steep), it’s obvious: run the first target into the second (it’s impossible for the shooter to ever make it there). If they’re side-by-side (flat), it’s obvious in the opposite direction: you’ll never get the first target moving sideways with enough speed to move the second rock, so you have to plan to use the shooter. At roughly a 45 degree angle (to the direction of the incoming stone) is where you’d make the switch from trying to line up the shooter to trying to line up the target to make the double.

Now, let’s circle back to that assumption about non-spinning discs in our physical model. There is something called the gear effect to bear in mind: the spin on the rocks will matter, at least a little.

Basically a rotation “in to” the target will see the shooter “bounce” more, giving a steeper and longer roll. Conversely, curling across the face of the target will see the shooter have a “dead” roll, with a flatter, shorter roll. {This part is in the book and the figure is there}

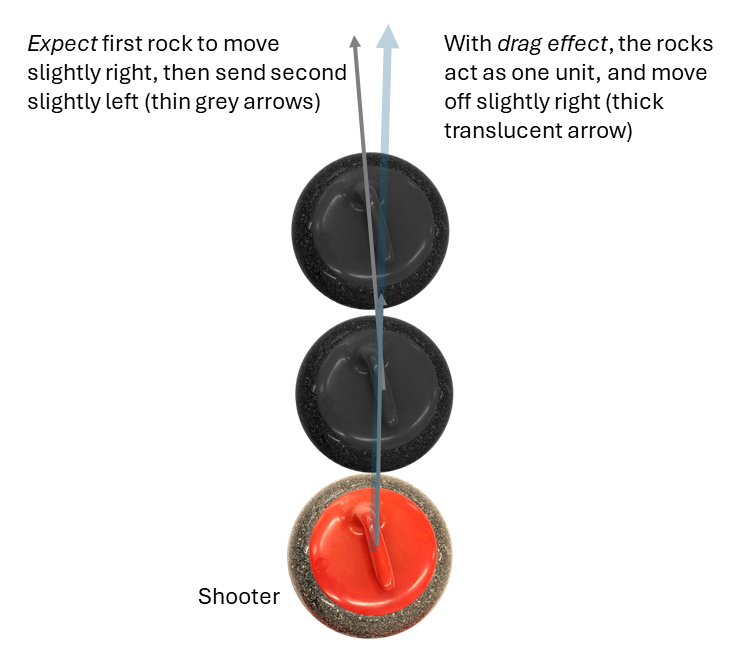
Finally, there’s one more weird physics-bending aspect of curling to mention: the drag effect. This is where if two stones are touching (or very close to touching), then instead of acting like two separate stones in a double-takeout situation, they may act as one combined stone: you’d draw your line through the centre of both together. So if you had these two stones nearly touching and hit from one side, you may expect the first stone to go off a bit to one side, hit the second stone, and send it straight back or perhaps a bit off the other way. Instead, the second stone also moves a bit in the direction the first stone is sent — the direction (or close to it) you’d get from thinking of them as one big oblong rock and connecting the centre (the point between the two) and the centre of the shooter to find your line.

[Added later]

Bonus Addendum to the Bonus Chapter

TimS from the Curling Discord server corrected me on my mental math that originally said a “half rock hit would roll out at a 45 degree angle.” It’s actually 60 degrees. Let’s go through the math for a few examples to see how it works (and how I should have done it in the first place).

Content warning: this section will involve middle school trigonometry!

We can set our collision up like this:

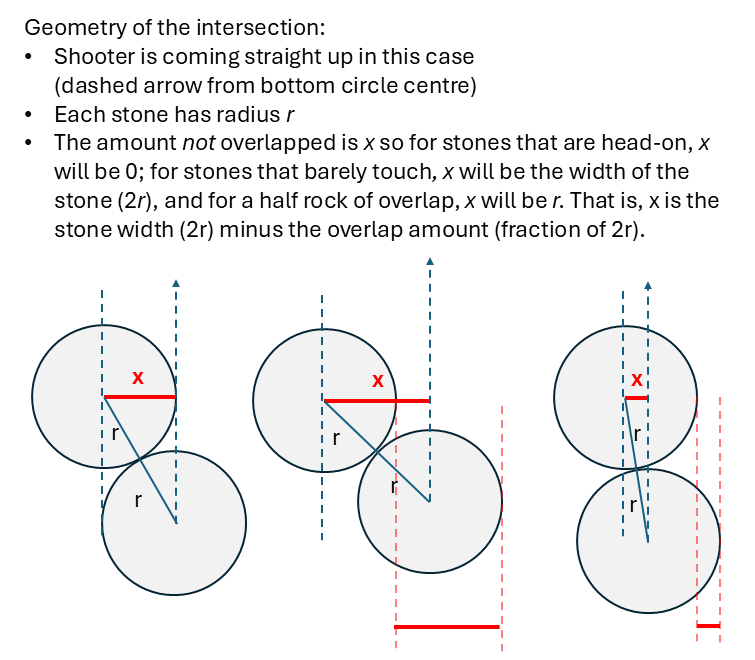
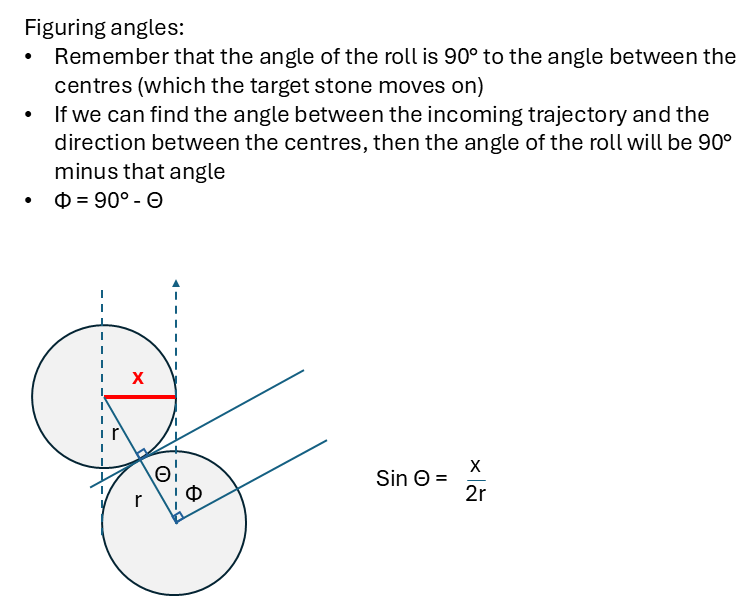
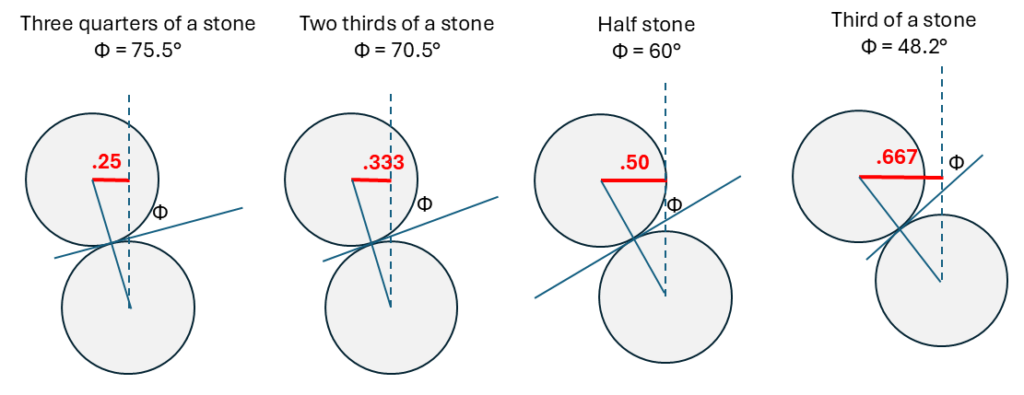
So we ultimately want to find the angle between our incoming rock and the trajectory it will roll out (the tangent of that collision), which is marked as Φ in the diagram. That angle is the complement of the one that the target will move along, the angle between the incoming stone and the line connecting the centre of the two. In the diagram, you can see a classic right-angle triangle with x as one side, and 2r as the hypotenuse. So trigonometry comes into play: the sine is opposite over hypotenuse. That is, sinΘ = x/2r. And x is the amount of non-overlap (the inverse of our overlap) in our collision: if we hit three quarters of a rock, x will be one quarter of a rock. Since a rock’s width is 2r, we can replace that as non-overlap/rockwidth and since they’re both fractions of a rock, x/2r becomes just the fractional amount of non-overlap.

That’s going to help us find Θ with just a tiny bit more math. Once we have that, we can find Φ, the angle of the roll, by subtracting Θ from 90°.

So if you hit “half a stone”, x/2r will be 1/2. That means we have sinΘ = 0.5. You can then plug that into a calculator or look it up to find that Θ = 30°. So if the angle our target moves off at is 30°, our shooter will roll at 90-30° = 60°.

Likewise, if you hit a quarter of a stone, x/2r will be 3/4. If you hit 3/4, then x/2r is 1/4, etc.

For quick future reference, if you hit:

A quarter of a stone: the shooter rolls out at 41.4°

A third of a stone: the shooter rolls out at 48.2° (so to get a 45° you want to hit just a hair less than two-thirds)

A half of a stone: the shooter rolls out at 60°

Two-thirds of stone: the shooter rolls out at 70.5°

Three-quarters of a stone: the shooter rolls out at 75.5°

Seven-eighths of a stone: the shooter rolls out at 82.8° (though there won’t be much roll with that solid a hit)